Pusat dapodik – Dalam kehidupan sehari-hari, kita sering menjumpai benda-benda yang berbentuk seperti balok. Misalnya penghapus, sabun, dan lain sebagainya. Dalam bentuk balok, kita juga mengenal istilah diagonal bidang dan diagonal ruang. Kali ini kita akan membahas rumus diagonal ruang dari suatu bangun yang disebut balok. Selain itu juga akan dibahas tentang rumus bidang diagonal bidang bangun geometri.
Diagonal ruang pada balok adalah ruas garis yang menghubungkan dua titik sudut yang berlawanan dalam suatu ruang. Untuk menghitung rumus diagonal ruang balok, Anda dapat menggunakan teorema Pythagoras.
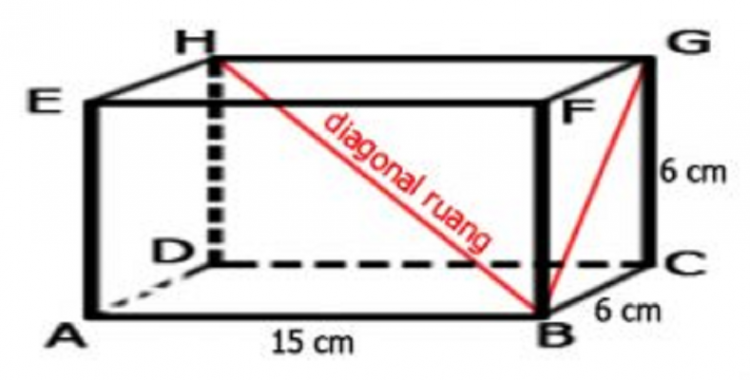
Berikut rumus diagonal ruang dan bidang balok
Rumus diagonal balok adalah:
b = √(p2 + l2)
Sedangkan rumus diagonal ruang balok adalah :
d = √(p2 + l2 + t2)
di mana:
b = bidang diagonal balok
d = ruang diagonal balok
p = panjang balok
l = lebar balok
t = tinggi balok
Agar anda dapat memahami definisi tersebut, maka anda dapat mencoba melihat gambar ini.
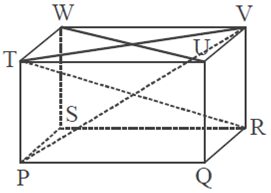
Anda dapat menghubungkan titik Q dan W, P dan V, S dan U atau R dan T. Garis RT, QW, PV dan SU adalah diagonal ruang. Diagonal ruang yang ada akan berpotongan di satu titik. Sebuah balok memiliki empat diagonal ruang yang sama panjang. Dan akan berpotongan pada satu titik.
Cara Menghitung Diagonal Ruang Balok
Misalnya, ada blok ABCD.EFGH. Balok itu memiliki panjang pslebar l dan memiliki ketinggian t. Dengan demikian, AG dapat dihitung dengan menggunakan teorema Pythagoras. Namun, sebelum melakukan perhitungan tersebut, terlebih dahulu kita harus mencari panjang AC. Dimana AC adalah diagonal sisi. Anda dapat mempertimbangkan segitiga ABC dan sudut siku-siku di B. Jadi:
AC = √(AB2 + BC2)
AC = √(p2 + l2)
Sekarang kita bisa mencari panjang AG menggunakan teorema Pythagoras juga. Anda dapat mempertimbangkan segitiga ACG yang sudutnya berada di G. Jadi:
AG = √(AC2 + CG2)
AG = √(√(p2 + l2)2 + t2)
AG = √(p2 + l2 + t2)
Jika ruang diagonal dalam bentuk persegi panjang adalah dmaka secara umum rumus menghitung diagonal ruang berbentuk balok adalah d = √(p2 + l2 + t2).
Contoh Soal Menghitung Diagonal Balok
Agar lebih jelas, kali ini kami akan membagikan contoh soal dalam menghitung rumus balok diagonal yaitu rumus diagonal ruang.
Sebuah balok berukuran panjang 12 cm, lebar 8 cm, dan tinggi 4 cm. Sekarang coba hitung berapa diagonal ruang balok tersebut.
Menjawab:
d = √(p2 + l2 + t2)
d = √(122 + 82 + 42)
d = √224
d = 4√14 cm
Balok Diagonal
Diagonal balok adalah bidang yang dibatasi oleh dua sisi dan dua diagonal balok. Untuk dapat menghitung luas bidang diagonal, kamu dapat menggunakan rumus luas persegi panjang.
Agar lebih paham, berikut contoh soal yang kami bagikan berikut penjelasannya.
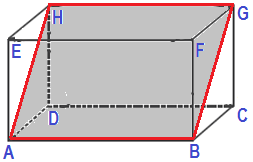
Diberikan balok ABCD EFGH. Diketahui panjang AB 12 cm, BC 8 cm, dan AE 6 cm. Jadi sekarang hitung luas bidang diagonal ABGH.
Pertama kita mencari panjang BG menggunakan teorema Pythagoras.
BG = √(BC2 + CG2)
BG = √(82 + 62)
BG = √(64 + 36)
BB = √100
BB = 10 cm
Luas diagonal ABGH adalah:
Luas ABGH = AB . BG
Luas ABGH = 12 cm. 10cm
Luas ABGH = 120 cm2
Bagaimana penjelasan rumus diagonal ruang dan luas pada balok tersebut? sangat mudah dipahami bukan?


















