pusatdapodik.com kali ini kita akan membahas pengertian, pengertian, rumus, dan contoh soal matematika diferensial beserta pembahasannya secara lengkap. Diferensial merupakan teori perubahan variabel, untuk lebih jelasnya simak penjelasan di bawah ini.
Definisi Diferensial
Turunan fungsi (diferensial) adalah fungsi lain dari fungsi sebelumnya, misalnya fungsi f menjadi f’ yang nilainya tidak beraturan. Derivatif (diferensial) digunakan sebagai alat untuk menyelesaikan berbagai masalah dalam geometri dan mekanika.
Konsep turunan sebagai bagian sentral dari kalkulus dipikirkan secara bersamaan oleh Sir Isaac Newton (1642 – 1727), seorang matematikawan dan fisikawan Inggris, dan Gottfried Wilhelm Leibniz (1646 – 1716), seorang matematikawan Jerman.
Turunan Matematika Adalah
Misalkan y adalah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x
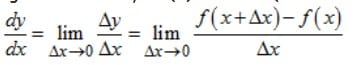
Formula Diferensial
Formula 1 :
Jika y = cxn dengan c dan n konstanta nyata
jadi dy/dx = cnxn-1
contoh :
y = 2×4 lalu dy/dx = 4,2×4-1 = 8×3
Rumus 2 :
Jika y = f(x) + g(x)
maka turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)
contoh:
y = x3 + 2×2 maka y’ = 3×2 + 4x
y = 2×5 + 6 maka y’ = 10×4 + 0 = 10×4
Rumus 3 :
Jika y = c di mana c adalah konstanta
jadi dy/dx = 0
contoh:
jika y = 6 maka turunannya sama dengan nol
Rumus 4 :
Turunan Perkalian dari Fungsi If yf(x).g(x)
jadi y’ = f'(x) . g(x) + g'(x) . f(x)
contoh:
y = x2 (x2+2) lalu
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
Kemudian masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4×3 + 4x (jawaban ini juga bisa diperoleh dengan mengalikan dulu lalu menggunakan rumus 2)
Rumus 5 :
ef(x) lalu dy/dx = ef(x).f'(x)
contoh :
y = e2x+1
f(x) = 2x+1
f'(x) = 2
maka f’ = e2x+1 . 2 = 2e2x+1
Rumus 6 :
Derivatif Trigonometri Sin
Jika Anda memiliki y = sin f(x)
maka turunannya adalah ie y’ = cos f(x) . f'(x)
contoh :
y = sin(x2 + 1)
maka y’ = cos (x2 +1) . 2x = 2x. cos (x2 +1)
Rumus 7 :
Turunan Trigonometri Cos
Jika Anda memiliki y = cos f(x)
maka turunannya adalah y’ = -sin f(x). f'(x)
contoh :
y = cos (2x+1)
maka turunan y’ = -sin (2x+1) . 2 = -2 sin (2x+1)
Rumus Turunan Kedua
Rumus turunan kedua sama dengan turunan pertama.
Turunan kedua diperoleh dengan mengurangkan turunan pertama.
Contoh :
Turunan kedua dari x3 + 4×2
turunan pertama = 3×2 + 8x
turunan kedua = 6x + 8
Contoh Soal Diferensial (Fungsi Derivatif)
Contoh Soal 1
Persamaan garis singgung kurva y = 2×3-5×2-x+6 yang memiliki absis 1 adalah …
Resolusi:
y = 2×3 – 5×2 – x + 6 → x = 1
y’ = 6×2 – 10x – 1
y (1) = 2(1)3- 5(1)2 – 1 + 6
= 2 – 5 – 1 + 6
= 2 → ( 1 , 2 )
y’ = m = 6×2 – 10x – 1
= 6(1)2 – 10,1 – 1
= -5
Persamaan tangen: y – b = m (x – 1)
y – 2 = -5 (x – 1)
y – 2 = -5x + 1
5x + y +3 = 0
Jawab : 5x + y + 3 = 0
Contoh Soal 2
Turunan pertama dari fungsi F(x) = Cos5(4x-2) adalah F'(x) = …
-5 Cos4 (4x-2) Dosa (4x-2)
5 Cos4 (4x-2) Dosa (4x-2)
20 Cos4 (4x-2) Dosa (2x-2)
10 Cos3 (4x-2) Dosa (8x-4)
-10 Cos3 (4x-2) Dosa (8x-4)
Menjawab :
F(x) = Cos5(4x-2)
u = Cos (4x-2) → u’ = -4Sin(4x-2)
n = 5
F'(x) = nun-1.u’
= 5 Cos5-1 (4x-2) . -4 Dosa (4x-2)
= 5 Cos4 (4x-2) . -4 Dosa (4x-2)
= -20 Cos4 (4x-2)Sin (4x-2)
= -10,2 Cos (4x-2)sin (4x-2) . Cos3 (4x-2)
= -10 Dosa 2(4x-2) Cos3 (4x-2)
= -10 Dosa (8x-4) Cos3 (4x-2)
= ( -4x+5) e-3x+4
Dengan demikian pusatdapodik.com jelaskan tentang matematika diferensial, semoga bermanfaat


















