
pusatdapodik.com kali ini kita akan membahas interpolasi yang meliputi rumus berbagai jenis interpolasi dan beberapa contoh soal interpolasi beserta jawabannya.
Definisi Interpolasi
Interpolasi adalah proses menemukan dan menghitung nilai suatu fungsi yang grafiknya melewati sekumpulan titik tertentu. Titik-titik tersebut mungkin merupakan hasil percobaan dari suatu percobaan, atau mungkin diperoleh dari fungsi yang diketahui
Interpolasi Perbandingan Segitiga
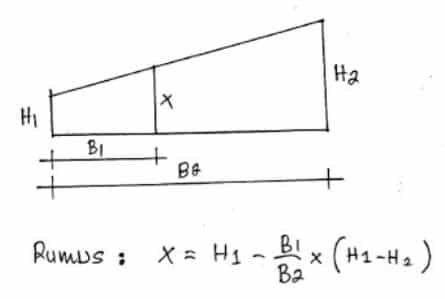
Contoh :
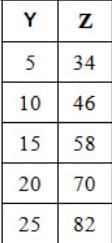
Jika Y = 17, berapakah nilai Z ?
Resolusi:
Nilai Y = 17 berarti diperoleh range antara 15 sampai dengan 20
dari tabel diperoleh:
H1=58
H2=70
B1=20-17=3
B2=20-15=5
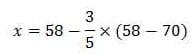
nilai x didapat = 65,20
Interpolasi Linier
Interpolasi linier adalah cara mendapatkan nilai antara dua data berdasarkan persamaan linier. Interpolasi linier adalah metode untuk menentukan nilai fungsi persamaan linier berdasarkan hukum proporsionalitas.
Rumus Interpolasi Linear
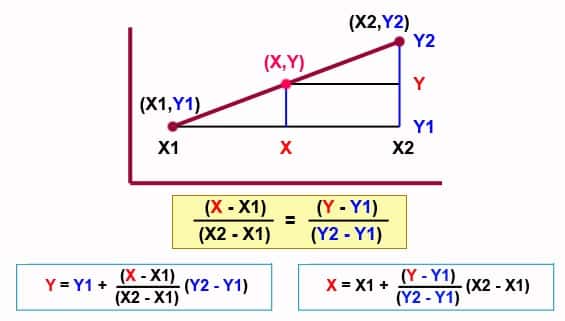
Contoh Cara Melakukan Interpolasi Linear
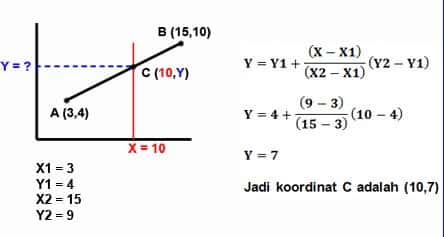
Pertanyaan: Diketahui bahwa pada suatu garis lurus yang melalui koordinat titik A (3,4) dan koordinat titik B (15,10) dalam sistem koordinat X dan Y. Garis AB memotong garis vertikal dengan persamaan X = 9 di titik C. Tentukan koordinat titik C.
Menjawab :
X1 = 3
Y1 = 4
X2 = 15
Y2 = 10
X = 9
Interpolasi dalam Statistik
Contoh:
Jika suatu penelitian mempunyai sampel 60 responden dengan derajat kebebasan yaitu n-2 = 58.
Pada tabel t, sangat sulit untuk mengkonsultasikan nilai dk 58 karena nilai 58 tidak dituliskan secara riil melainkan antara dk 40 dan dk 60 sehingga perlu dilakukan nilai 58 pada tabel.
Perhitungan interpolasi dilakukan dengan menggunakan rumus di bawah ini:
Rumus Interpolasi dalam Statistik
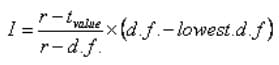
Deskripsi rumus:
Saya = nilai interpolasi
r-nilai = rentang (selisih) nilai t pada tabel dari dua dk terdekat
Untuk contoh di atas nilai dk 58 adalah pada dk 40 dan dk 60, nilai t untuk dk 40 pada tabel adalah 1,684 sedangkan nilai t untuk dk 60 adalah 1,671.
Maka selisih nilai t adalah 1,684 – 1,671 = 0,013
rd.f. = jarak (selisih) dua dk terdekat
Selisih dari dua nilai dk terdekat adalah 60 -40 = 20
Kemudian nilai interpolar dimasukkan sebagai nilai yang dikurangi dari nilai t untuk dk terdekat yang paling rendah. Hasil ini kemudian digunakan sebagai nilai t untuk dk yang tidak tercantum dalam tabel.
Maka perhitungannya adalah:
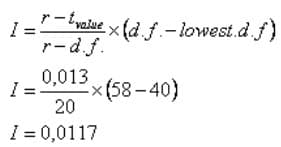
nilai t untuk dk 58 = nilai t untuk dk 40 – I
= 1,684 – 0,0117
= 1,6723
Interpolasi Kuadrat
Interpolasi Kuadrat digunakan untuk mencari titik diantara 3 titik
P1(x1,y1), P2(x2,y2) dan P3(x3,y3) menggunakan pendekatan fungsi kuadrat
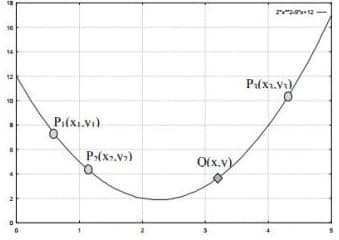
Untuk mendapatkan titik Q(x,y) digunakan interpolasi kuadrat sebagai berikut:
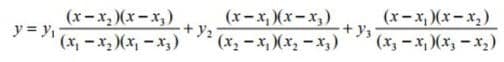
Interpolasi polinomial
Sayainterpolasi polinomial digunakan untuk mencari titik tengah dari n titik P1(x1,y1), P2(x2,y2), P3(x3,y3), …, PN(xN,yN) menggunakan pendekatan fungsi polinomial pangkat n -1:
![]()
Masukkan nilai setiap titik ke dalam persamaan polinomial di atas dan dapatkan persamaan simultan dengan n persamaan dan n variabel bebas:
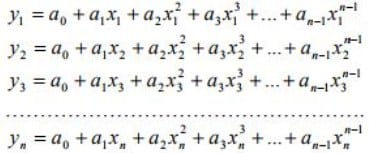
Penyelesaian persamaan simultan di atas adalah nilai a0, a1, a2, a3, …, an yang mana
adalah nilai koefisien dari fungsi pendekatan polinomial yang akan digunakan. Dengan memasukkan nilai x dari titik yang Anda cari dalam fungsi polinomial, Anda akan mendapatkan nilai y dari titik tersebut.
Demikian penjelasan interpolasi, semoga bermanfaat





